Simulating Speciation

When we look out at the world around us, we inevitably see a large amount of life, with many extremely different forms between species. We can describe these life forms that can interact locally as species in a community, and hence the main issue for modelling this community is disentangling the nature of the interactions. All the species are distinct, so modelling the species themselves is straightforward. QED.

If you are not the least bit skeptical of that last statement, let me reassure you; it is a blatant lie.

Take introgression between moth species (Valencia-Montoya et al., 2020). Here, the story roughly goes, farmers in Brazil contend regularly with a local moth, Helicoverpa zea. In 2013, the farmers had a new problem: Helicoverpa armigera. You see, the pesticides that the farmers used for H. zea were not effective against H. armigera¹, but the farmers were not aware of that. The natural thing to do when they saw a sudden outbreak was to increase their pesticide usage, which selected for H. armigera. Aside from the obvious consequence though, it gets worse. H. armigera’s resistance to the local pesticide is contained in a single gene and H. armigera proceeded to hybridize with H. zea. Valencia-Montoya et al. analysed the genome and saw that, despite what we might expect from distinct species, the hybrids successfully brought this gene back into the H. zea population. Furthermore, the species evidently remained distinct otherwise using comparisons from 2017. This is an example of adaptive introgression, but also of the fuzziness of the species concept.

H. zea (left, credit: public domain from Wikipedia.) and H. armigera (right, credit: Donald Hobern, licensed under CC BY 2.0). If you are like me, you probably cannot tell these two apart either². I think the right has better aviator shades though.

So what are species? And more importantly, can we operationalize it enough to measure it? The former question is unsurprisingly complicated given the above, but worth looking at. Singh gives an overview, borrowing from Mayr and Ashlock as well as Wilkins (Wilkins, 2006; Singh, 2012). Singh presents four overarching (historical) concepts of species, as well as Wilkins’ list, which itself includes at least twenty more specific concepts. The first general concept is the typological species concept where species are static and distinct. This is useful over short time scales in a simulation, but is obviously a large simplifying assumption. Next is the nominalistic concept, where “species” is an invented, but unphysical, category. While true in some sense, e.g. the ever on-going reorganisation of taxonomic rank or the boundary paradox (Podani, 2009), it neglects that these clusters do exist and such categorizations are useful³.

Next is the biological species concept, which focuses on groups at the reproductive, ecological, and genetic levels. This is perhaps closest to what we might naively expect, as the critical test occurs “only where populations belonging to different species come into contact” (Mayr, 1982, p. 286; Singh, 2012). In principle, one could test this in an individual based simulation by comparing any two communities, but it is not obvious where to draw a line. Finally, this concept does not cope well with evolutionary intermediacy, for which the evolutionary species concept was developed. Wiley describes a species as a “single lineage… which maintains its identity from other such lineages and which has its own evolutionary tendencies and historical fate” (Wiley, 1978). On the one hand, this is arguably a taxon, but, on the other, species are a valid taxon and we can look for the emergence of separate identities using clustering for instance.

So what is the naive mathematician to do? One obvious consequence is that there is some degree of opinion or outside parameter we will inevitably need to incorporate into the model. We can tune and play with this parameter, but full objectivity is probably not possible it would seem. How have others dealt with this problem? Gavrilets (2014) has a useful review. For example, we might think of species as clusters of individuals in a genotype space, the abstract space where a point indicates a specific genotype. These individuals die and reproduce, causing the clusters to change over time. In turn, the clusters can fragment to form new species-clusters. Fragmentation is only possible if there is variability in a cluster that can grow as well as the reduction or elimination of gene flow between subpopulations of a species-cluster. This still requires some way of recognising species as distinct clusters, but agrees (in various ways) with the above concepts.

In practice, this leaves a few questions that we need to answer for our model. First, how do we implement reproductive isolation? Second, at what point do we declare speciation to have occurred?

Unsurprisingly, both questions have a variety of answers (Gavrilets, 2014). For example, one might model genetic incompatibilities directly, using the Bateson-Dobzhansky-Muller model in which mutations from the original genotype in separate populations prevent the new genotypes from mating. Modelling genetic incompatibilities has also shown that there is a fairly sharp and sudden crossover between reproductive compatibility and isolation due to the “snowball” and “threshold” effects. Hence, using a genetic distance directly has been a common simplifying assumption. More complicated models make use of gene networks to better model the incompatibilities.

Genetic models usually assume that genes do something, but what happens if they do not? While obviously controversial, see so-called junk DNA, neutral models have been surprisingly adept at modelling biodiversity. The historical way to model speciation neutrally is to have offspring randomly at low fixed probability belong to a different species from the parents, although more recent work uses less controversial speciation models.

Another option that makes use of familiar mathematical tools like random walks, game theory, and differential equations is adaptive dynamics (Dieckmann and Law, 1996). Speciation here becomes evident at “branching points” in the system where multiple strategies are taken by the system (Kisdi, 1999; Doebeli and Dieckmann, 2005). While not necessarily speciation by itself, since reproductive isolation is inferred, one could explicitly add it in using “magic traits”, i.e. traits that are both reproductive and adaptive.

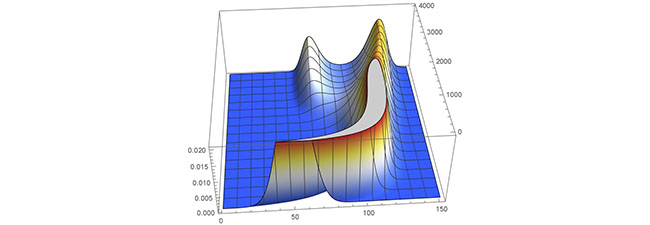
An example of evolutionary branching produced in Mathematica 12 reproducing example 3 from Kisdi 1999. Height corresponds to the amount of population present, which is truncated in the image for presentation. The horizontal axis corresponds to values of the trait, while the depth axis corresponds to time. The two species branch from each other due to multiple optimal strategies.

There are other options of course, but this seems like a good place to end the overview. Where does it leave us? There are the usual trade-offs between complexity and tractability, especially considering the usefulness of neutral theory. There is also a need to decide if speciation is an explicit process or an implicit (nominalistic?) pattern. As always when modelling, consider the system and questions you are wanting to address. After all, modelling is a way of thinking about problems and “[t]he choice, then, is not whether to build models; it's whether to build explicit ones” (Epstein, 2008).

Endnotes
1. Evidently, H. armigera is notoriously insecticide resistant with Valencia-Montoya et al. observing that they have “the highest number of reported cases of insecticide resistance worldwide” alongside a list of insecticides to which they are resistant (Valencia-Montoya et al., 2020).
2. Morphologically, Valencia-Montoya et al. indicate they are quite similar, but they have different reproductive appendage sizes and different food preferences.
3. Conceptually, one could engage with this idea using simulations still. Start with an original cluster of reproductive individuals that define a taxon. Subject the cluster to selection and evolution. As this concept says, the species you infer from the simulation are human created if you do not put in hard speciation barriers (e.g. cannot interbreed if genetic distance exceeds some specific amount), but instead use, e.g., clustering to segregate the population into different species.