Contemplating contingency

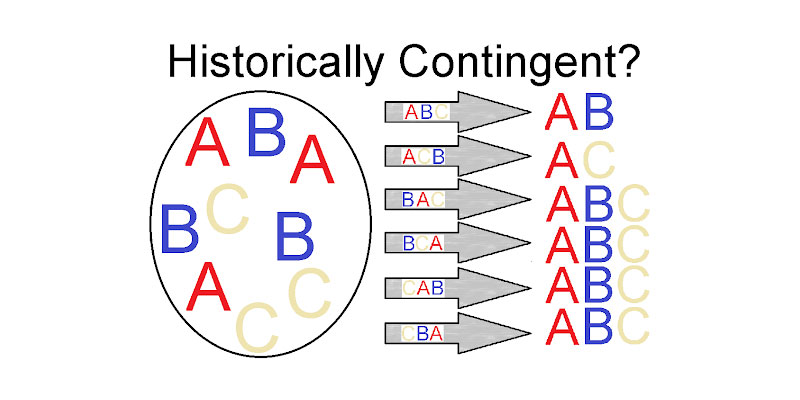
History is perhaps unsurprisingly controversial, especially recent history. Elections are one good example and it is common to hear about election post-mortems from or about the losing party (e.g. Bacon, 2021). These sorts of exercises are often thought experiments made to better understand events and a situation, but even the act of thinking about these thought experiments can be controversial in history. This topic of historical contingency is present in many disciplines. In history, the topic is usually counterfactual history. In biology, I have come across it as priority effects and historical contingency. The central premise is fairly simple. Since time only flows in one direction for us and we only have one realisation of it, how are we to judge alternative realisations? Can such alternative realisations help us to better understand the realisation that actually occurred?

Now, as a matter of full disclosure, I should note that I am a mathematician by training. My PhD looked at mathematical modelling of historical data. My colleagues (which include historians) and I published a paper on the usage of bootstrapping to make counterfactual Battles of Britain (Fagan et al., 2020) and managed to get a fair amount of media response (and associated comment sections) (e.g. Pinkstone, 2020). By background, I am firmly on the side of “counterfactuals are useful tools if used precisely”. This is a deep topic in each field that thinks about it, and I have tried to give a quick survey below.

Different disciplines struggle with these historical contingency in different ways, largely due to how reproducible their experiments are. When there is no potential for divergent variation, think simple local kinematics experiments like rolling a ball down a ramp, there is no problem; every “alternative” is the same. At the other end, when every "experiment" is unique it quickly becomes hard if not impossible to consider alternative results.

Consider bowling: modelling the return of the bowling balls is an extremely deterministic process. Modelling the movement of the bowling balls down a lane has a bit more variation, but has general rules that we can use to understand it, such as the gutters. Modelling any individual person, however, becomes extremely specific. While there are general rules we could use to understand people’s behaviour, each person behaves in a fairly unique and very historically contingent fashion. Image credit: Public Domain from Wikimedia Commons.

Community ecology has a bit of a history with this problem. Consider a pool of species which can invade a given environment. Does the order of their arrival matter for the “final” community? The answer is sometimes, and this gets into the problem of priority effects, which has been foundational for researchers like Fukami. From a practical side, one might reasonably find that the environment fully determines the final community. There might be some variation here or there in the order of migrants, but the final community matches the environment perfectly, an idea that Fukami states stems back to Clements’s 1916 piece on Plant Succession and Clements’s discussion of a climax community (Fukami 2010, page 47).

On the other hand, consider a neutral theory of community assembly, where each species, perhaps of a given trophic level, is effectively interchangeable while still being separate species. Clearly there must be some structure to this community, e.g. no primary consumers without producers, but the order of arrival and the ability to competitively exclude (or otherwise prevent new arrivals from getting a foothold) becomes crucial to the final community. This results in multiple possible realities or stable communities separate mostly through random chance. (Fukami refers to Lewontin’s 1969 piece on stability as the standard citation (2010, page 47).) Both types of systems (and even systems that lack a final community entirely) can be explored theoretically using models of community assembly (e.g. Law and Morton, 1996; Morton and Law, 1997; Coyte et al., 2021). There is also reason to believe that there are both historically contingent and deterministic communities on some form of spectrum. Chase has argued for both using, for example, data on ponds to argue for multiple alternative stable communities (Chase, 2003). On the other hand, research done by Coyte and colleagues found that assembly of preterm infant dental microbiota communities was highly deterministic and explicitly constructed a theoretical assembly system to study how such determinism could be achieved (Coyte et al., 2021).

History intrinsically is about the study of experiments that only happened once, albeit in a comparative light. Much of the focus is on establishing what the ground truth is followed by comparison (history “rhymes”) and causality. Counterfactual analysis is not generally considered an acceptable tool in this field. For example, Evans has discussed extensively some of the flaws of counterfactual analysis in history, including the tendency of some users of the technique to introduce chance everywhere or to make utopias or dystopias as fits their wants (Evans, 2016). Indeed, introducing even a small amount of “natural” chance can have apparently big changes.

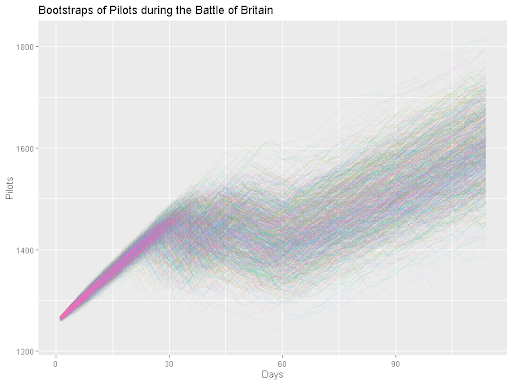
Borrowing from work done on bootstrapping the Battle of Britain, we can consider pilot populations if we were to resample daily losses with replacements (see Fagan et al. 2020 for details). The x-axis is days since the Battle of Britain simulations began and the y-axis is the adjusted number of pilots (to account for differences in training) with each transparent line an individual simulation. One problem with counterfactuality is that even in this restrained case we can see the overall variation in populations grow. This occurs due to both the day-to-day variation and the accumulation of this variation, resulting in large differences even when just considering the actual data. Of course, this does not address whether these differences on their own are large enough to change the course of the Battle.

In history, the problem is roughly that there is rarely a clear and explicit model for how reality would have behaved if something small was changed, and yet there is also an appeal in “for want of a nail” scenarios. Small changes should most commonly make for small differences, but there are always examples such as a driver taking a wrong turn. To combat this, there has been an effort to better define how counterfactuals should work, such as describing the difference between exuberant counterfactuals, where change compounds upon change to rewrite history, and restrained counterfactuals, where a single change is examined for its influences on future events (Megill, 2004). There has even been a write-up of proposed rules for how counterfactuals should be constructed (Tetlock and Belkin 1996, page 18). These rules help to create restrained counterfactuals and require clarity, logical consistency (no violating cause and effect or other counterfactual assumptions), minimal rewrite (keep as close to reality as you can), theoretical consistency (no violating how we know or believe reality works), statistical consistency (no flukes of luck), and projectability (in the sense of comparability with other real world events).

Mathematics is, in principle, removed from this debate, but it does creep in. A classic example where counterfactual analysis is considered is proof by contradiction. The idea is that, in order to prove something true, you prove that if it were otherwise there would be a logical contradiction. A more useful example to the average person might be that probability and statistics deal with realisations of random variables. Random variables encode the randomness in a system and are how we conceptualise results that we might otherwise refer to as random. Despite their randomness they have well-defined properties. Of particular use are Central Limit Theorems, which characterize how randomness can naturally lead to similar outcomes. At the same time, typical central limit theorems have constraints such as having a mean or a limit to how much the random variables vary. Some random variables (such as power law distributions) do not always obey this and can lead to black swans that the rules for counterfactuals above specifically ignore despite their very real repercussions (Taleb, 2007). It is also worth noting that counterfactual analysis is growing as a subject in causal mathematics, albeit already with major (and at times acrimonious) splits between those supporting Judea Pearl’s vision of the field (Pearl, 2000; Little and Badawy, 2019) and those supporting the vision of Imbens (who was just jointly awarded the Nobel economics prize for his work in this field) (Imbens and Rubin, 2015; Imbens and Menzel, 2018).

Coming from a STEM background, my view has always been that we can make use of counterfactuals and counterfactual reasoning, but I think the different disciplines above have done good jobs of trying to discuss the limits. From biology, we know there are good reasons to expect both deterministic and stochastic effects in the world. Random flukes do happen, but most random flukes do not matter for the course of history or experiment. From our knowledge of history, it usually requires a whole new experiment to investigate random flukes of any significance. History also helps inform us as to how counterfactuality can be approached. Unless these random flukes are truly paradigm shifting, they should be consistent with what we know about the world. Trying to extract any more than that rapidly becomes exuberant, and it is not far from there to the principle of explosion.

Bibliography

Bacon, P., Jr (2021) Why the Republican party isn’t rebranding after 2020, FiveThirtyEight. Available at: https://fivethirtyeight.com/features/why-the-republican-party-isnt-rebranding-after-2020/ (Accessed: 1 October 2021).

Chase, J. M. (2003) ‘Community assembly: when should history matter?’, Oecologia, 136(4), pp. 489–498. doi: 10.1007/s00442-003-1311-7.

Coyte, K. Z. et al. (2021) ‘Ecological rules for the assembly of microbiome communities’, PLoS biology, 19(2), p. e3001116. doi: 10.1371/journal.pbio.3001116.

Evans, S. R. J. (2016) Altered pasts: Counterfactuals in history. London, England: Abacus.

Fagan, B. et al. (2020) ‘Bootstrapping the Battle of Britain’, The Journal of military history, 84(1), pp. 151–186.

Fukami, T. (2010) ‘Community assembly dynamics in space’, in Verhoef, H. A. and Morin, P. J. (eds) Community Ecology: Processes, Models, and Applications. Oxford: Oxford University Press, pp. 45–54.

Imbens, G. and Menzel, K. (2018) ‘A Causal Bootstrap’, arXiv [stat.ME]. Available at: http://arxiv.org/abs/1807.02737.

Imbens, G. W. and Rubin, D. B. (2015) Causal Inference in Statistics, Social, and Biomedical Sciences. Cambridge University Press. Available at: https://play.google.com/store/books/details?id=Bf1tBwAAQBAJ.

Law, R. and Morton, R. D. (1996) ‘Permanence and the Assembly of Ecological Communities’, Ecology, 77(3), pp. 762–775. doi: 10.2307/2265500.

Little, M. A. and Badawy, R. (2019) ‘Causal bootstrapping’, arXiv [cs.LG]. Available at: http://arxiv.org/abs/1910.09648.

Megill, A. (2004) ‘The New Counterfactualists’, Historically Speaking, 5(4), pp. 17–18. doi: 10.1353/hsp.2004.0072.

Morton, R. D. and Law, R. (1997) ‘Regional Species Pools and the Assembly of Local Ecological Communities’, Journal of theoretical biology, 187(3), pp. 321–331. doi: 10.1006/jtbi.1997.0419.

Pearl, J. (2000) Causality: Models, Reasoning, and Inference. Cambridge: Cambridge University Press. Available at: https://play.google.com/store/books/details?id=wnGU_TsW3BQC.

Pinkstone, J. (2020) 'Germany could have WON the Battle of Britain if they started earlier, study finds’, Daily mail, 10 January. Available at: https://www.dailymail.co.uk/sciencetech/article-7872831/Germany-WON-Battle-Britain-started-earlier-study-finds.html (Accessed: 1 October 2021).

Taleb, N. N. (2007) The Black Swan: The impact of the highly improbable. Random house.

Tetlock, P. E. and Belkin, A. (1996) ‘Counterfactual thought experiments in world politics: Logical, methodological, and psychological perspectives’. Princeton University Press.