2.3.3 Verification of the learned model
Practical guidance - cross-domain
Authors: John Grese and Dr Corina Pasareanu (CyLab, Carnegie Mellon University)
Neural network verification for safety-critical applications
Deep neural networks (DNNs) are used increasingly in safety-critical applications such as autonomous transport. However, it has been shown that DNNs can produce unsafe predictions when adversarial or unexpected inputs are provided [3], which raises serious safety concerns. To address these concerns, DNNs need to be extensively tested and verified to ensure that they meet important safety requirements. Formal verification methods based on Satisfiability Modulo Theory (SMT) [1][5] and Mixed-Integer Linear Programming (MILP) [6][7] can provide sound assurances that no adversarial examples exist within a given neighbourhood of an input. We discuss here how formal verification tools, such as Marabou [1], in conjunction with clustering techniques, can be used to evaluate a network’s sensitivity and robustness against small perturbations to provide better safety guarantees. This entry is based on [4].
Local robustness
Local robustness can be characterised by the minimum perturbation (𝜹) applied to an individual input (𝒙) which causes a change in the network’s prediction. Formal verification tools can be used to both discover the minimum value of 𝜹 which causes the change in prediction, and to prove the network is robust with respect to a specified 𝜹. Local robustness can be useful in understanding how much a given input can be changed (possibly by an adversary) before the network’s prediction will change. Equation 1 describes the formal guarantee provided by local robustness checks, which states that for any 𝒙′ such that the distance from the input 𝒙 is less than 𝜹, the network will produce the same output.
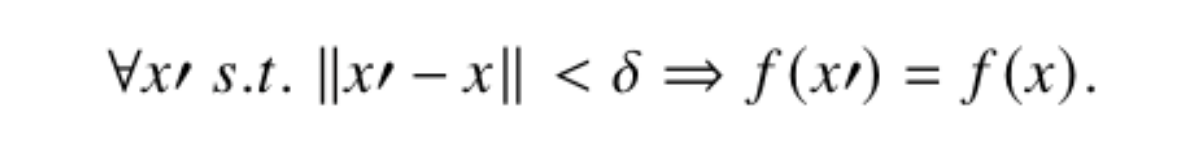
Equation 1
Targeted robustness
Targeted robustness can be characterised by the minimum perturbation (𝜹) applied to an input (𝒙) which causes a specific change in the network’s prediction. In the case of a classifier, this could mean that a specific label does not exist within the verified region 𝒙 ± 𝜹. For example, consider a classifier which predicts the driver’s reaction time as slow, medium or fast. In a classifier such as this, targeted robustness checks could be used to prove that a fast input will not be labelled as slow within the radius 𝒙 ± 𝜹. This would be helpful in providing guarantees that the worst-case prediction does not occur within a specified 𝜹. The formal guarantee provided by targeted robustness can be seen in equation 2, which states that for all 𝒙′ with a distance from 𝒙 less than 𝜹, the target does not exist.
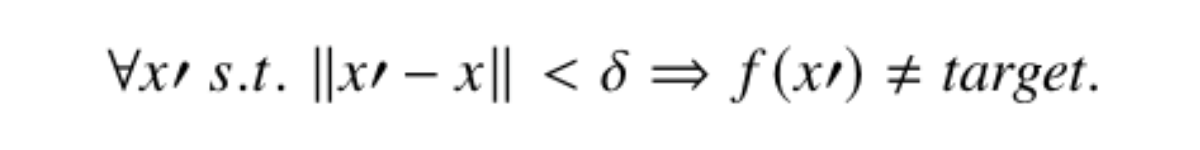
Equation 2
Sensitivity
Sensitivity is similar to robustness, but is characterised by the minimum perturbation (𝜹) applied to an individual feature, i.e., input component 𝒙i, of a given input 𝒙 which causes a change in the network’s prediction. A smaller 𝜹 indicates that the network is more sensitive to changes in feature 𝒙i, and a larger 𝜹 indicates that the network is less sensitive. Using formal verification for this type of analysis on a network’s sensitivity has the benefit of providing formal guarantees that no adversarial inputs exist within the specified 𝜹. Formal verification tools can be used to both discover the minimum value of 𝜹, and prove that the network is robust within a specified 𝜹. Using the discovered value 𝜹, one can infer how sensitive a given feature is to adversarial perturbations, and also gain insight into the importance of the feature with respect to the network’s prediction. Equation 3 describes the guarantee provided by formal verification on a given feature 𝒙i of input 𝒙 with respect to the minimum perturbation 𝜹.
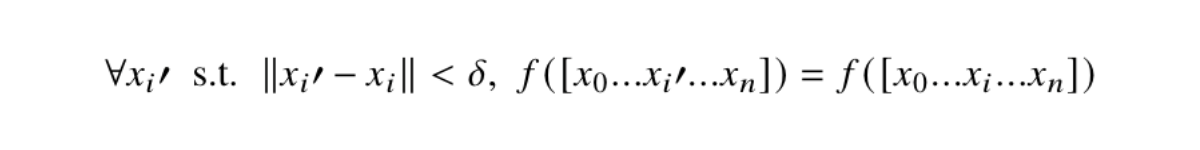
Equation 3
An asymmetric variant of sensitivity checking can be performed to identify how the network behaves with respect to positive vs negative perturbations to 𝒙i. In an asymmetric sensitivity test, a feature 𝒙i is perturbed by independent values for the negative and positive perturbations (𝒙i-𝜹neg and 𝒙i+𝜹pos). The asymmetric sensitivity analysis can yield additional information about the model, and can identify biases in the network.
Data-driven verification
Both sensitivity and robustness (including targeted robustness) can be checked automatically with a formal verification tool like Marabou [1]. However, the obtained guarantees are only for small regions around individual points, in which the network is proven to produce the same output. Data-driven verification techniques such as DeepSafe [2] can be used to provide assurances that no adversarial inputs exist within larger regions of the input space. Essentially, the technique performs clustering on the dataset to identify regions with similar points that have the same label. Figure 4 shows an example of a clustering algorithm called “Label Guided K-Means” [2] which produces regions containing a single label.
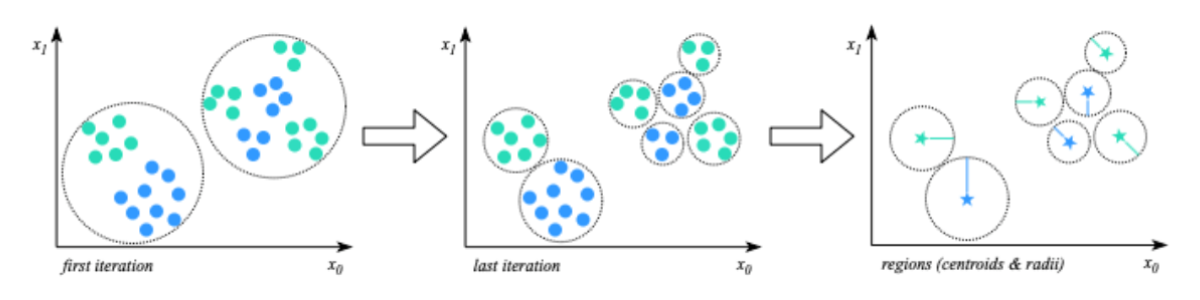
Figure 4: Regions containing a single label produced by “Label Guided K-Means”
Each region produced by Label-Guided K-Means has a centroid, which can then be used as target for verification, with respect to robustness or targeted robustness. The resulting 𝜹 discovered from the verification of the region’s centroid can then be used to calculate the “verified radius” of the region. Using the centroids and verified radius r, we can produce a set of “safe regions” which have been formally verified, and proven to contain points of a single label. Intuitively, we expect these regions to be larger than the ones verified through the local robustness checks, since they come from clusters of multiple inputs with the same label. An example of these safe regions is shown in figure 5. The coloured regions illustrate the formally verified “safe regions”.
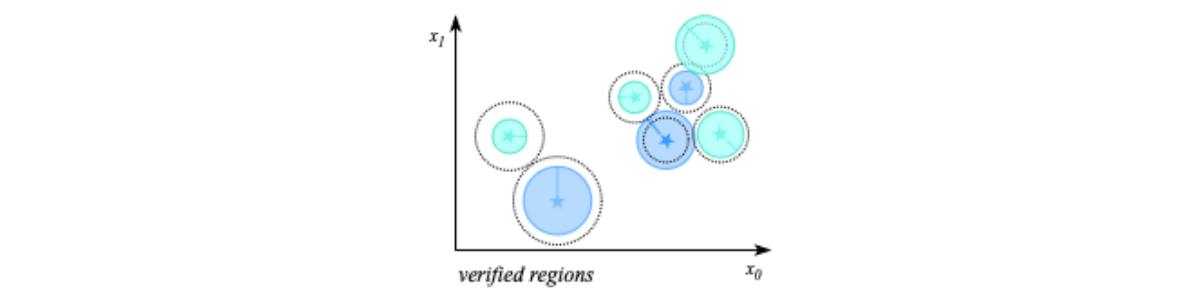
Figure 5: Example of formally verified “safe regions”.
The “safe regions” provide the guarantee described by equation 6, which states that for all 𝒙 such that the distance from the centroid is less than the verified radius r, the network will produce the same label. This method can also be generalised to support different types of distance metrics and networks [2].
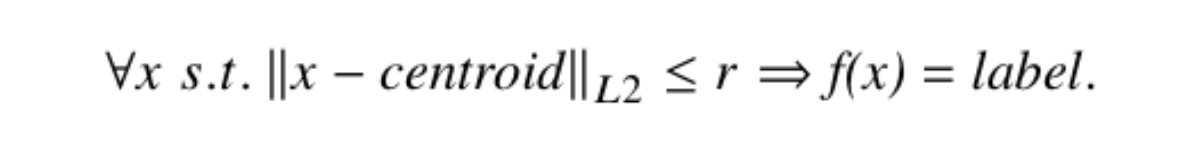
Equation 6
Verification results
Formal verification tools for neural networks typically accept input-output queries as specifications, and provide counterexamples when the queries do not hold. These counterexamples can help improve understanding of the network’s behaviour; furthermore, they can be amplified and used to improve robustness and sensitivity through retraining the network. The verified “safe regions” (obtained with the data-driven verification) describe portions of the input space in which the network behaves as expected; they can be potentially used as run-time “guards” during network deployment or can be provided to safety controllers in a searchable format to provide a measure of confidence about the network’s predictions.
References
- [1] Katz, G., and et al., “The Marabou Framework for Verification and Analysis of Deep Neural Networks”, CAV, 2019.
- [2] Divya Gopinath, C. S. P. C. B., Guy Katz, “DeepSafe: A Data-driven Approach for Checking Adversarial Robustness in Neural Networks,” ATVA, 2018.
- [3] Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., and Fergus, R., “Intriguing Properties of Neural Networks,” ICLR, 2014.
- [4] Grese, J., Pasareanu, C., and Pakdamanian, E., “Formal Analysis of a Neural Network Predictor in Shared-Control Autonomous Driving”, to appear in 2021 AIAA SciTech Forum.
- [5] Katz, G., Barrett, C., Dill, D., Julian, K., and Kochenderfer, M., “Reluplex: An Efficient SMT Solver for Verifying Deep Neural Networks”, CAV, 2017.
- [6] Ehlers, R., “Formal Verification of Piece-Wise Linear Feed-Forward Neural Networks”, ATVA, 2017.
- [7] Botoeva, E., Kouvaros, P., Kronqvist, J., Lomuscio, A., and Misener, R., “Efficient Verification of ReLU-Based Neural Networks via Dependency Analysis,” Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 34, 2020, pp. 3291–3299.
Contact us
Assuring Autonomy International Programme
assuring-autonomy@york.ac.uk
+44 (0)1904 325345
Institute for Safe Autonomy, University of York, Deramore Lane, York YO10 5GH
Related links
Download this guidance as a PDF:
Contact us
Assuring Autonomy International Programme
assuring-autonomy@york.ac.uk
+44 (0)1904 325345
Institute for Safe Autonomy, University of York, Deramore Lane, York YO10 5GH
Related links
Download this guidance as a PDF: