• Study
• People
• Research and innovation
  • Communication technologies
  • Condensed matter and materials physics
  • Healthcare engineering
  • Intelligent systems and robotics
  • Nuclear Physics
    • Computing Nuclei
    • Hadron and nuclear physics
    • Nuclear Astrophysics
    • Nuclear Symmetries
    • Neutron-Rich Nuclei
    • Shapes and Fission
    • NSTAR 2024
    • Events
  • Physics of Life
  • Quantum science and technologies
  • Fellowships
  • Early Career Researchers Forum
• Public and schools
• About us
• Contact us
• Current staff and students

Proton-neutron Symmetries In Exotic Nuclei

Our recent key publications

Discovery of 72Rb: A Nuclear Sandbank Beyond the Proton Drip Line. PHYSICAL REVIEW LETTERS 119, 192503 (2017)

The role of core excitations in the structure and decay of the 16(+) spin-gap isomer in Cd-96. PHYSICS LETTERS B767, 474-479 (2017)

Isospin Symmetry at High Spin Studied via Nucleon Knockout from Isomeric States: PHYSICAL REVIEW LETTERS 117, 082502 (2016)

The proton and the neutron can be considered as two states of the same particle, referred to as the nucleon. This is because the attractive nuclear force is virtually the same, regardless of which type of nucleon are involved. For a pair of mirror nuclei, where the number of neutrons in one matches the number of protons in the other, one therefore may expect their properties to be essentially the same. This symmetry, referred to as isospin symmetry, is manifestly violated by electromagnetic force as the proton has a positive charge and the neutron is neutral.  Since the electrostatic repulsion between protons is well understood, its effects on the nucleons can be calculated precisely and so any other significant differences observed for mirror nuclei may be attributed to other elusive forces that violate isospin symmetry. For example, it is well known that the nuclear force, at least when measured in free space, is not quite charge symmetric  - that is, the neutron-neutron interaction is just a bit stronger than the proton-proton interaction. We are interested in how this “charge-asymmetry”, and any other “isospin-violating” forces, manifest in the nuclear medium. Thus, our studies shed light on one of the most basic aspects of the nuclear force – the strongest of the fundamental forces.

Figure 1. Nuclei with interchanged numbers of neutrons and protons exhibit near-identical behaviour.

Our Physics

The York group leads a number of experimental programmes around the world studying the effects of these forces through creating, and comparing, sets of  “isospin symmetric” nuclei. The simplest example is the mirror pair, with exchanged numbers of neutrons and protons. We have studied many mirror pairs to understand these forces – a recent example can be found in Phys. Rev. Lett. 117, 082502, (2016).  Another key aspect of our work is the study of isospin triplets. An isospin triplet is a set of three nuclei one of which is an odd-odd N=Z nucleus, and two other neighbouring even-even nuclei with Z+1, N-1 and Z-1, N+1. An example is the triplet ⁷⁴Rb (Z=37,N=37) and its even-even neighbours ⁷⁴Sr (Z=38,N=36) and ⁷⁴Kr (Z=36,N=38). We have studied this triplet recently (Phys. Rev. C 90, 051303(R) 2014). As can be seen in figure 2, the energy level schemes for the three nuclei are nearly identical. This occurs since the nuclear force is nearly charge-independent, and the structure of the three nuclei is essentially identical, except for exchanges of protons for neutrons (from left to right in fig 2). The small differences observed, at the few keV level, can be attributed to subtle isospin-violating forces. 

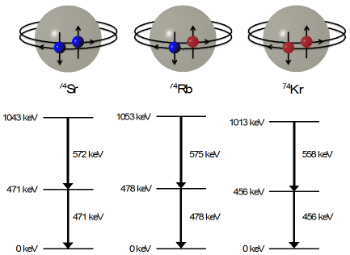
Figure 2. The A=74 isospin triplet which we have studied (Phys. Rev. C 90, 051303(R) 2014). The energy level schemes for the three nuclei are nearly identical. This occurs since the nuclear force is nearly charge-independent, and the structure of the three nuclei is essentially identical, except for changes of protons into neutrons (left to right).

Pairing is of crucial importance in nuclear physics – this is the strong attractive interaction between pairs of nucleons, moving in time-reversed orbits, that creates extra nuclear binding and has a stabilising effect on the structure of atomic nuclei.  Normally, we only consider pairing between like nucleons (i.e. pp or nn pairing). However, since the nuclear force is almost charge independent, we should also expect to pairing to occur between neutrons and protons (np pairing). This does indeed happen, and is observed in N=Z nuclei in particular (see the picture at the top of figure 2).  However, as opposed to pairs of “like” nucleons, np-pairs do not have to obey the Pauli principle when they interact, and this can yield new and exotic types of np-pairing and np-correlations. At York, we study these different ways that neutrons and protons couple together, ways that are forbidden for like-nucleon pairs. A high profile example is Nature 469, 68–71 (2011).  

In N=Z nuclei, the symmetry between protons and neutrons can also yield structures which are based strongly on clusters of alpha-particles (each having two protons and two neutrons). Staff at York also investigate the occurance of this phenomenon (e.g. J. Phys. G, Vol. 42, No. 3, 034010, 2015).

In all of these studies, we also apply, at York and with our collaborators, state-of-the-art theoretical calculations to attempt to understand our observations. At York, we run both shell-model (e.g. Phys Rev C 92, 024310, 2015)
and more recently Density-Functional Theory calculations (arXiv:1510.04831 [nucl-th] 2015) to tackle these complex issues.

Figure 3. A schematic diagram showing how fragmentation beams can be used to create exotic proton-rich nuclei. Here the reactions we used a ⁵⁸Ni beam to make a secondary beam of radioactive ⁵³Co. In a second step, a neutron is knockout out of the ⁵³Co beam to create ⁵²Co in an excited state.  The diagram shows how these reactions move away from the “valley” of nuclear stability.

Our Experiments

To study these effects, we need to create nuclei which are either on the line of N=Z, or have more protons than neutrons (proton-rich nuclei). This is extremely difficult to do since these nuclei are very far from stability. The study of proton-rich nuclei requires some sophisticated experimental techniques, many of which have been developed by the York group. At the University of Jyväskylä, Finland, we create the proton-rich nuclei in “fusion-evaporation” reactions, and identify the very weak reactions of interest (leading to the proton-rich nuclei) through identifying, and tagging on, the characteristic radioactive decays of the exotic nuclei created. At other facilities, e.g. GANIL in France, we again use fusion reactions, but this time we identify the proton-rich nuclei by measuring the fast neutrons that are emitted at the point that the nucleus of interest is made. At the National Superconducting Cyclotron Laboratory, Michigan, we create our exotic nucleus of interest in a two-step reaction. First we take a relativistic beam of stable nuclei (e.g. ⁵⁸Ni), perform a fragmentation reaction to make an unstable nucleus nearer to the nucleus of interest, then separate and identity this using a magnetic spectrometer, and fire that onto another target. Here, our final proton-rich nucleus is made by knocking out one or two further neutrons.  An example is shown schematically in Figure 3, showing how we used a reaction ⁵⁸Ni -> ⁵³Co -> ⁵²Co to study the properties of the proton-rich ⁵²Co system.  In all of these reactions, we need to measure the gamma-rays associated with the decays of the excited states we have populated.  To do this, we surround the reaction target with large arrays of gamma-ray detectors, usual hyperpure Ge crystals. Figure 4 shows one of these arrays. This is the GRETINA array, in the USA, which we have used for our studies and which tracks gamma-ray interactions through the Ge crystals to allow for precision gamma-ray spectroscopy.