Dr Martin Bates
01904 324474
Email: martin.bates@york.ac.uk
Simulation of liquid crystals and complex systems
We are the theory and simulation arm of the York Liquid Crystal Group. Our research is into the understanding of self-organising and self-assembling materials at the molecular level. By building models of molecules and using computers to simulate the behaviour of bulk systems, we can investigate how different interactions influence the phase behaviour and hence the properties of materials.
The systems studied vary from small molecules which exhibit the common nematic phase used in many liquid crystal displays, to bent core molecules which exhibit biaxial phases, to large flexible supermolecules that contain a number of groups, designed to have specific properties. We are also interested in mixtures, be they polydisperse mixtures in which the components have a range of sizes, or discrete mixtures of only two or three components, such as those formed by mixing rod shaped and disc shaped molecules.



Snapshots taken from a simulation of rod shaped molecules, exhibiting an isotropic (disordered) phase, a nematic (orientationally ordered) phase and a smectic (positionally ordered or layered) phase.
Recent work has concentrated on how the biaxial nematic phase can be stabilised in bent core molecules. In particular we have been interested in determining how molecular features such as flexibility and dipoles can change the stability of the biaxial nematic phase. Flexibility tends to destabilise biaxiality whereas a transverse dipole induces biaxiality.
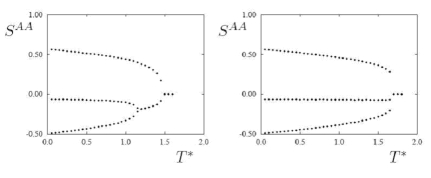
Components of the ordering tensor for a bent core molecule with a (left) weak and (right) strong transverse dipole as a function of temperature. Where there are two distinct values in the ordering tensor, the phase is uniaxial nematic; where there are three distinct components, the phase is biaxial nematic. This shows that adding a dipole to this model shifts the biaxial nematic transition to higher temperatures, squeezing out the uniaxial nematic phase, and leads to a first order isotropic – biaxial nematic transition.

