


The formation of nitrogen oxides by electrical discharges and implications for atmospheric lightning
M. S. Stark, C. Anastasi, and J. T. H. Harrison
Department of Chemistry, University of York, York, Y01 5DD, United Kingdom
Journal of Geophysical Research, Vol. 101, no. D3, pages 6963-6969, March 20, 1996
Copyright 1996 American Geophysical Union
Abstract. The mechanism of production of nitrogen oxides by electrical discharges has been examined. The velocity of shock fronts generated by laboratory scale discharges have been measured and are found to be too slow to raise the air temperature to the ca. 3000K necessary for nitrogen fixation by the Zel'dovich mechanism. The freeze out mixing ratio of NOx in air has been measured directly for low pressure discharges and is found to be of the order expected from the Zel'dovich mechanism for gas cooling over a timescale far longer than the duration of the shock front. Therefore it is concluded that NOx is formed in the gas in the slowly cooling hot channel region and not in the rapidly cooling shock front. Also, it is argued that NOx formation occurs by a freeze out mechanism due to a rapid drop in temperature, not density as has been suggested. NO2 production is found to be significant, with the [NO2]/[NO] ratio being strongly dependent on the water content of the air. Discrepancies between previous experimental studies of the [NO2]/[NO] ratio and the quantity of NOx formed per unit energy (P) are discussed. P is also found to vary with spark gap and ambient pressure. It is thought that these effects may be due to significant loss of heat from the spark gap to the electrodes. The inclusion of atmospheric levels of N2O, CH4 and CO2 are found to have no measurable effect on the yields of NO or NO2.
Introduction
Nitrogen oxides or NOx (NO, NO2) play a key role in the photochemistry of the atmosphere and their removal by precipitation is a potential natural source of fixed nitrogen for the biosphere. Thus the rate of production of nitrogen oxides by natural and anthropogenic sources has been of great interest in recent years. It has been suggested that lightning is a major natural source of NOx, although there is considerable uncertainty over both the magnitude and mechanism of NOx production by the hot gases produced by a lightning discharge [Noxon, 1976; Tuck, 1976; Griffing, 1977; Chameides et al., 1977; Chameides, 1979; Hill, 1979; Hill et al., 1980; Dawson, 1980; Levine et al., 1981, 1984; Peyrous and Lapeyre, 1982; Drapcho et al. 1983; Borucki and Chameides, 1984; Franzblau and Popp, 1989; Liaw et al., 1990; Goldenbaum and Dickerson, 1993].
One approach to the calculation of the global production of NOx (NO + NO2) by lightning is to measure the global energy dissipation by this phenomenon and then multiply this by the amount of NOx generated per unit energy (P) by electrical discharges in controlled laboratory experiments [Chameides et al., 1977; Levine et al., 1981; Peyrous and Lapeyre, 1982]. Estimates of global NOx production of 3-30×1034 NOx molecules per year have been made using this technique [Borucki and Chameides, 1984]. The uncertainty is to an extent a result of the uncertainties in measuring P.
A potential problem with this method is that in terms of energy per unit length and total length of discharge, laboratory electrical discharges have tended to be smaller than atmospheric discharges. Atmospheric discharges can be over 104 m long, depositing 104-105 J m-1 [Dawson, 1980], while laboratory discharges range from 10-2 to 1 m with energy depositions of 101 to 105 J m-1 [Chameides et al., 1977; Levine et al., 1981; Peyrous and Lapeyre, 1982]. The theoretical analysis of Chameides et al. [1977, 1979] has attributed NOx formation by lightning to the heating of air in the vicinity of the discharge channel by the strong shock front generated by the discharge, with the NOx being formed via the Zel'dovich mechanism [Zel'dovich and Raizer, 1966]. A consequence of this analysis is that there should be a weak dependence of P on the energy per unit length of the discharge, justifying the use of laboratory determinations of P for atmospheric scale discharges. Chameides [1979] calculated that P would only increase by a factor of two, as the discharge energy per unit length increased from 1 to 104 J m-1.
However there has been some controversy recently as to whether NOx is formed in the shock front, with Hill et al. [1979, 1980] suggesting, on the basis of numerical simulations of lightning, that due to the long duration of the discharge, the resulting shock wave never travels sufficiently fast for the gas just behind the front to get hot enough to fix nitrogen. It was suggested that NOx formation was occurring as the gases in the hot channel slowly cool as they mix with surrounding air.
In the present work, the formation of nitrogen oxides by laboratory scale discharges has been examined, to try to help clarify the mechanism of formation by lightning, which is not as amenable to study. The velocity of the shock front generated by laboratory scale discharges has been examined experimentally. The close relationship that exists between shock front velocity and the temperature rise across the front allows the temperature generated by the shock waves to be determined.
The Zel'dovich mechanism assumes that as the hot gases cool, an equilibrium NO concentration for a high temperature is "frozen out", giving a significant NO yield. For this work, the NO freeze out concentration has been directly determined, by addition of NO to an N2:O2 mixtures in which a discharge is fired. It has been suggested recently [Goldenbaum and Dickerson, 1993] that NO is formed by the Zel'dovich reactions, but that the freeze out of NO is due to a rapid drop in density during the onset of the discharge, not a drop in temperature. This suggestion is discussed in the light of the results from the present study.
Lightning occurs in regions of the atmosphere that vary greatly in their water content and ambient pressure, so the effect of these variables on NO and NO2 formation by laboratory discharges was also examined, as was the effect of the trace gases CO2, N2O and CH4.
Experimental
In the present work a discharge could be struck between two tungsten electrodes having a gap of 2 - 20 mm. The electrodes had a diameter of 4 mm, narrowing down to 2 mm diameter hemispheres 5 mm from their ends. The pyrex reaction vessel had a volume of approximately 250 cm3 and was generally spherical apart from two optical flat windows to allow the passage of a laser beam across the discharge.
Electrical discharges of energy 31 to 113 J and energy per unit length of 0.4 to 1.1×104 J m-1 were examined. A 2 microFarad capacitor was connected across the electrodes and could be charged up to 15 kV, with the discharge being struck by increasing the voltage until breakdown occurred. However, there was a slight run-to-run variation in the breakdown voltage using this technique so a thyratron trigger device was put in the circuit between the capacitor and one of the electrodes, to achieve a more reproducible discharge for the NO freeze out mixing ratio experiments. The capacitor could then be reproducibly charged to potentials above the breakdown voltage, with the discharge occurring when the thyratron was triggered. The thyratron was not used in the other experiments however, because of the possibility that some of the energy from the capacitors was dissipated in the thyratron and not between the electrodes. All the discharges were fired in dry air (BOC), except for those described in (figures 3 and 5, to which known quantities of NO (Matheson) and water vapour were added.
NO or NOx (sum of NO and NO2) was detected by flushing the contents of the reaction vessel through a chemiluminescence NOx detector (Thermoelectron Corporation, Model 10A). The detector was calibrated by analyzing for known concentrations of NO or NO2. There was an uncertainty in the NOx measurements of ca. 2-4 ppb NOx, which translates to the error bars shown in figures 3-5. There was also an uncertainty in measuring the breakdown voltage of ca. 200 V, which contributes a ca. 5% uncertainty to the measurements of NOx per unit energy and energy per unit length.
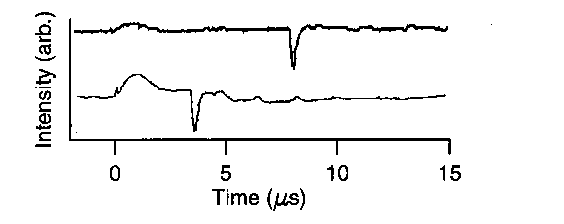
The radial velocity of shock fronts generated by electrical discharges was examined using a simple laser deflection technique. A narrow beam (0.3 mm diameter) from a 633 nm HeNe laser was directed across the reaction vessel in the plane centred on the mid-point of the spark gap, perpendicular to the axis of the electrodes and at known distances from the axis of the electrodes. The shock front consists of a shell of dense gas which causes a change in refractive index of the air and hence a deflection of the laser beam, when the front reaches the beam. The laser beam was directed onto the edge of a photodiode 2 m from the reaction vessel. The small angle of deflection of the beam by the shock front caused the beam to move slightly off the diode, giving a reduction in signal. The light intensity recorded by the diode was stored on a digital oscilloscope. The examples given in figure 1 show the diode signal for the laser at a distance of 6 and 12 mm from the axis of the electrodes. The signal in the first 2 microseconds is due to light from the spark reaching the diode and can be used to estimate an upper limit for the duration of the current flow in the discharge. With the laser beam 6mm from the axis of the electrodes there was a decrease in signal due to the arrival of the shock front 3.5 microseconds after the start of the discharge, taken to be when the light from the discharge starts. With the laser beam 12 mm from the electrode axis the decrease in signal due to the arrival of the shock front at the beam occurs 7.8 microseconds after the start of the discharge. The delay between the start of the discharge and the deflection of the beam increases as the distance of the beam from the discharge increases (figure 2); the velocity of the shock front is then determined from the gradient.
The NOx freeze out mixing ratio was determined by adding varying concentrations of NO to an N2:O2 mixture and monitoring the increase or decrease in NOx formed when a discharge was fired. Ideally, these freeze out mixing ratio experiments would have been conducted at pressures at which lightning occurs (200 mbar to 1.0 bar). However for two reasons the experiments had to be conducted at lower pressures. Since the NO freeze out mixing ratio is proportional to the difference between two large numbers (NOx measured with and without a discharge), the uncertainty in [NO]freeze out is proportional to pressure and reliable measurements could not be determined above 70 mbar. Secondly, with higher pressures of NO, the NO added to the N2:O2 mixture undergoes significant conversion to NO2 (via the termolecular reaction NO + NO + O2) before a discharge can be fired. Where NO2 was present in measurable amounts, there was an anomalous slight increase in NOx produced by the discharge, as more NOx was added. Two possible reasons for this are, firstly, any NO2 present can thermally dissociate to NO and O atoms at lower temperatures than the NO freeze out temperature, or secondly there is photolysis of NO2 to NO and O by UV light from the discharge. These additional sources of O atoms could lead to the additional NOx observed.
Results
The velocity of shock fronts propagating away from the electrical discharges was measured at 200 and 500 mbar and with spark gaps of 4 to 20 mm. Figure 2 gives the distance travelled by the front against time for the 500 mbar cases. The measured velocity close to the discharge is similar for both the 4 and 20 mm spark gaps, but the velocity of the former decreases with increasing distance more than in the 20 mm case. For the latter, the highest shock front velocity measured was (2200±200) m s-1, found by using the time for the front to travel from 2 to 4 mm from the spark gap centre. The shock front is unlikely to be faster at earlier times than those measured, as this would require the front to start with zero radius sometime after the start of the discharge. The front velocities for the other pressures and spark gaps examined were all less than or similar to this value. A radius for the luminous channel of approximately 2.5±1.0 mm was estimated by photographing the discharge through optically thick filters (20 mm spark gap, 500 mbar pressure). This value is ca 70±30% of the radius of the shock front at 1.9 µs, the end of the luminous discharge.
The NOx freeze out mixing ratio was determined as (2.8±0.4)% (figure 3) and (2.3±0.3)% at 27 and 67 mbar; however, as discussed in the next section, there is some evidence of interference from the reactor walls in the higher pressure experiment.
The variation with spark gap of the NOx produced per unit energy (stored on the capacitor) was significant as shown in figure 4 (previous work is shown for comparison and is discussed below). The variation in the yield of NOx with pressure was also examined, with the yield of NOx per joule increasing by 45% on increasing the pressure from 0.13 to 1.0 bar and the [NO2]/[NOx] ratio remained constant at 0.46±0.04 (8 mm spark gap). The variation in the NOx and NO2 yields with water content is given in figure 5. For dry air the [NO2]/[NOx] ratio is high at 0.52±0.07, decreasing significantly with increasing water content. The addition of atmospheric concentrations of CO2, N2O and CH4 was found to have no measurable effect on NOx or NO2 production by the discharge.
Discussion
NOx formation via the Zel'dovich mechanism.
Nitric oxide formation by electrical discharge is thought to be via the Zel'dovich mechanism. At high temperatures the gas mixture heated by the discharge is thought to be in chemical equilibrium, with the equilibrium concentration of NO, ([NO]equil.(T)) decreasing as the temperature decreases (figure 6). If the gas mixture maintained chemical equilibrium as it cooled to ambient temperature, then the quantity of NO formed would be insignificant as [NO]equil. at 300 K is very low. However, the time constant for the rate at which the gas approaches chemical equilibrium (tauequil.(T)) is also very strongly dependent on temperature, and increases as the gas cools. For example, from figure 6, at 3000K, 500 mbar, tauequil. = 10-3 s, therefore if the gas is cooling sufficiently slowly that taucooling > 5×10-3 s the NO concentration follows the equilibrium NO concentration as the gas cools. When the gas has cooled to the extent that tauequil. is approximately equal to taucooling, the equilibrium NO concentration for this temperature is "frozen out". Further cooling of the gas results in the rate of approach to chemical equilibrium being much slower than the rate of cooling of the gas, so the NO concentration no longer follows the equilibrium NO concentration below this freeze out temperature, Tfreeze out, ie.
[NO]freeze out = [NO]equil.(Tfreeze out) (1)
where Tfreeze out is determined by the condition such that,
tauequil.(Tfreeze out) = taucooling (2)
The number of NO molecules produced by the discharge is simply the volume of gas heated to the freeze out temperature multiplied by [NO]freeze out.
Any NO2 production has either been thought to be insignificant, or due to conversion of NO to NO2 after the gas has cooled to well below the freeze out temperature: the total number of NOx molecules produced has therefore been taken as the amount of NO formed by the Zel'dovich mechanism.
Shock heating versus channel heating for NOx formation
It has been suggested that NOx formation occurs in the shock front that is generated by the rapid release of energy that occurs when an electrical discharge is fired [Tuck, 1976; Chameides et al., 1977; Chameides, 1979; Levine et al., 1979]. The amount of NOx formed was calculated by assuming that the bulk of the gas entrained by the shock front was compressed into a region just behind the shock front, so the temperature and rate of cooling of the bulk of the gas could be approximated by the temperature behaviour at the shock front [Tuck, 1976; Chameides et al. 1977; Chameides, 1979]. The behaviour of strong shock waves has been calculated by Lin [1954] for an idealised, instantaneous release of energy along a line source and this allowed Chameides [1979] to find the rate of cooling of the gas at the shock front (taucooling). Thermochemical and kinetic calculations of [NO]equil. and tauequil. allowed the freeze out temperature (Tfreeze out) and NO mixing ratio, and hence the amount of NOx formed by the discharge (P), to be calculated via equations 1-2.
However, Hill et al. [1979, 1980] have, on the basis of numerical simulation of lightning, suggested that due to the relatively long duration of the energy release (10 - 100 µs), the resulting shock front is not well represented by the analysis of Lin, which assumes an instantaneous release of energy, and is not energetic enough to reach the temperatures required to fix nitrogen. It was instead suggested that NOx was formed predominantly in the hot channel region of high temperature and low density well behind the shock front.
The question of whether the resulting shock fronts do raise the air temperature sufficiently to fix nitrogen can be addressed by monitoring the velocity of the front as it propagates away from the discharge. The close relationship that exists between the shock velocity and the temperature jump across the shock, given by the Rankine-Hugoniot equations [eg. Chorlton, 1967], allows the shock front temperature used in Chameides analysis to be determined experimentally:
Ts [2gamma M2 - (gamma - 1)][2 + (gamma - 1)M2]
-- = ------------------------------------------ (3)
To [(gamma + 1)2M2]
where To is the ambient temperature and Ts is the temperature just behind the shock front, gamma is the ratio of specific heats, and M = U/c, where U is the velocity of shock front and c is the velocity of sound in unperturbed gas.
The maximum shock front velocity from figure 2 is 2.2×103 m s-1 and given that gamma = 1.335 at ca. 2000 K and a = 330 m s-1 at 300 K [Zel'dovich and Raizer, 1966], the maximum temperature immediately behind the shock front would be 2480 K. This temperature would be sufficient to produce NOx if it was maintained for a sufficiently long time. However, from figure 6, tauequil.(2480 K) 6×10-2 s whereas taucooling < 10-5 s for the shock front (from the decrease in the front velocity with time from figure 2), the air entrained by the shock front is not at 2480 K for long enough for significant NOx production to occur. A temperature of greater than 4500 K is required to give tauequil. < 10-5 s, corresponding to a shock velocity of greater than 3600 m s-1. The measured velocities are well below this value, so for these experiments, NOx formation is unlikely to be by shock heating. Nevertheless, NOx is still produced in significant quantities by these discharges, suggesting that formation is occurring in the hot channel region as suggested by Hill et al.
Also shown for comparison on figure 2 is the radial propagation of the shock front as calculated by Hill [1971] using a channel heating model, and by Lin [1954], which assumes an instantaneous linear release of energy, and on which Chameides theory of NOx formation by lighting shock fronts is based. Lin's theory greatly overestimates the radial velocity of the front, while the calculations of Hill give velocities closer to the experimental values. The comparison is reasonable considering that both the energy per unit length and ambient pressure used in Hill's calculation are twice as high as used in the experiments. However, because no information has been obtained in this work on the energy or density distribution behind the shock front, it is not possible to determine from these experiments the fraction of the total discharge energy that is released as kinetic energy of the shock front. Nevertheless, it is not necessary to have a detailed description of the discharge development to refute the suggestion that NOx is formed by the shock front in these experiments, as the temperature immediately behind the shock front can be determined solely from the Rankine-Hugoniot relationship which depends only on gamma and the front velocity.
Some further evidence for this model was presented by Picone et al. [1981] who used Schlieren photography to examine the time development of the hot channel of a 15 cm, 600 J m-1 discharge. As the shock front was recorded in the first few photographs, the maximum observed front velocity can be determined as approximately 500 m s-1 (ca. 30µs after start of discharge), again, too slow for NOx formation in the front.
Density versus temperature freeze out of NOx
Goldenbaum and Dickerson [1993] have recently suggested that the previously accepted mechanism for NOx formation, whereby a high concentration of NOx is frozen out by a rapid drop in temperature is not appropriate for lightning. They suggest that NOx is frozen out by a rapid drop in density in the core region, causing the time constant for approach to chemical equilibrium (tauequil.) to increase significantly. It was also suggested that the key parameter for determining the NOx yield was the energy per unit volume deposited by the discharge and not the energy per unit length; further, they found a strong dependence of NOx yield per unit energy on the energy density. These conclusions were based on an analysis of numerical simulations using a hydrodynamic model coupled to a chemical model consisting of the three main Zel'dovich reactions.
However we believe their conclusion that NO is frozen out by a rapid drop in density, not temperature, is not appropriate for lightning for the following reasons. Their conclusion relies on there being a rapid drop in density in the core at the temperatures at which NO could form, say 3000 - 6000 K. This was achieved in their calculations by starting the simulation with a finite energy density over a given radius. This leads to an initial temperature in the region of ca. 6000 K, combined with a high (ambient) gas density. The resulting high pressure causes a shock wave to move away from the discharge, carrying most of the gas from the channel with it. This causes a slow reduction in the temperature and a rapid drop in gas density in the core. The total NO produced rose rapidly to a peak in ca. 1 µs then dropped slowly. The calculated chemical lifetime of NO increased rapidly, freezing out a high concentration in the first few microseconds; the increase in lifetime is caused by the rapid drop in density following the onset of the integration, and not the much slower decrease in temperature of the core.
In a lightning discharge however, the rapid drop in gas density in the core is accompanied by very much higher temperatures (over 20,000 K) than found in Goldenbaum and Dickerson's calculations. For example, Plooster's calculation [1971] of the gas behaviour following a spark discharge found that shortly after the time of maximum current flow, the core temperature was 30,000 K, with a core density already as low as 1/20th of ambient. Consequently the drop in core density in lightning is accompanied by a large rise in temperature, so the lifetime of NO will actually be decreasing rapidly as the density drops, precluding any freezing out of NO at this stage of the discharge process. Therefore we would maintain that NOx is formed by a freeze out mechanism due to the reduction in temperature in the core region.
Freeze out [NOx] mixing ratio
Zel'dovich et al. [1947] added quantities of NO to N2:O2 mixtures that were heated by combustion to greater than 2000 K and found that when NO was added to the initial mixture in large quantities, it decomposed, whereas with addition of small quantities led to an increase in concentration. The NO freeze out mixing ratio can be determined directly by finding the concentration of NO that needs to be added to give no net change in NO concentration. A similar experiment has been conducted in the present work, by adding small quantities of NO to N2:O2 mixtures in which an electrical discharge is struck.
Since [NO]freeze out is equal to the equilibrium NO concentration at the freeze out temperature (Tfreeze out), Tfreeze out can be determined from calculations of [NO]equil.(T). In addition, at the freeze out temperature, the time to achieve chemical equilibrium tauequil. will be equal to the time constant for the cooling of the gas (taucooling), so calculations of tauequil. allow taucooling to be determined. Finally, since the total number of NOx molecules produced by the discharge is determined, the volume of unperturbed gas heated to Tfreeze out can be calculated.
From figure 3, the equilibrium NO mixing ratio for a pressure of 27 mbar is (2.8±0.4)% (v/v). That an equilibrium was observed is strong direct evidence that NOx formation is occurring via the Zel'dovich mechanism. From figure 6, this value corresponds to a freeze out temperature of ca. 2900±400 K with a time constant for the cooling of the gas at this temperature of between 10-2 s and 0.4 s. The time constant for the cooling of the gas in the shock front is ca. 10-5 s, so again, these results do not support the suggestion that NOx formation occurs in the shock front. Likewise the time constant for the drop in density in the core during the onset of the discharge will be ca. 10-6 s, so these results are not consistent with the density freeze out mechanism of Goldenbaum and Dickerson.
Parameters effecting the yield of NOx per joule
An NOx freeze out mixing ratio of (2.3±0.3)% was also determined at 67 mbar pressure, using a much smaller reaction vessel (volume = 21.5 cm3) to circumvent some of the problems previously mentioned. However, for this case, the calculated volume of unperturbed gas heated to the freeze out temperature was comparable with the volume of the reactor, implying that some of the heat in the gas could be lost to the reactor walls, even while the gas temperature was high (above 2000 K), giving a reduction in NOx formed. This was confirmed by firing discharges with the same conditions in both the small and large reactors, the larger reactor produced approximately twice as much NOx per unit energy stored on the capacitor (P). Increasing the reactor size above 250 cm3 had little further effect on the NOx yield.
A more common problem with laboratory determinations of P is heat loss to the electrodes. This was examined in two ways. Firstly, when the electrode diameter was increased from 4 to 12 mm, the quantity of NOx formed was found to be reduced by a factor of two, even though all other parameters remained fixed. Secondly, the spark gap was increased from 4 to 20 mm (figure 4) giving a three fold increase in NOx formed per unit energy (stored on the capacitor). This behaviour is consistent with some of the energy of the gas being lost to the electrodes. This has in fact been demonstrated by Roth et al. [1951] who measured the decay with time of the fraction of heat (F) remaining in the gas between a spark gap. As the heat is lost (ideally) along only one space coordinate, F was determined in terms of a universal dimensionless parameter upsilon, which is the product of the thermal diffusivity constant, K (0.18 cm2s-1 for O2 at STP), the time since the discharge, t, divided by the square of the spark gap, d2:
Kt
upsilon = -- (4)
d2
F(upsilon) approaches 100% as upsilon approaches zero and for 4.6 mm diameter electrodes they found that F(upsilon) drops to ca. 10% for upsilon ca. 0.5.
Assuming that all the energy from the capacitor is transferred to the gas in the spark gap initially, the quantity of NOx formed (N) will be the product of the yield of NOx per joule (P) and the fraction (F) of energy (½CV2) remaining in the hot channel by the time it has cooled to the freeze out temperature:
N = ½CV2FP (5)
The time (t) for the gases in the hot channel to cool to the freeze out temperature is not known, but assuming a value of ca. 10-1 s the fraction of heat remaining in the gas between the spark gap can be determined from Roth et al's analysis as approximately 10% for a 4 mm spark gap, rising to 50% for a 20 mm gap (using t = 10-2 s gives F(4mm) = 35%, rising to F(20mm) = 70%).
Also, increasing the ambient pressure from 0.13 bar to 1.0 bar gave an increase in NOx per unit energy of 45%. In the analysis of Roth el al. [1951] the heat loss dimensionless parameter, upsilon, is dependent on pressure via the thermal diffusion constant K which is inversely proportional to the pressure. Using their relationship between F and with an assumed value of t of 10-1 s gives F = 15% at 130 mbar rising to 40% at 1013 mbar (for t = 10-2 s, F(130 mbar) = 45%, rising to F(1 bar) = 65%).
Due to uncertainties in the time to cool to the freeze out temperature, this analysis cannot be used to accurately determine F (and consequently P). However significant loss of heat to the electrodes is consistent with both our comparatively low measured values of NOx per unit energy stored on the capacitor, and its increase with increasing spark gap and pressure, and again suggests that the gas in which the NOx is formed is cooling far slower than either the duration of the discharge or the shock front.
The main circuit element that effected NOx formation was the thyratron, removing it from the circuit increased the NOx yield per unit energy (stored on the capacitor) by a factor of 2.5. The implication is that a significant fraction of the energy stored on the capacitor was not transferred to the spark gap, but to the thyratron. Consequently, the thyratron was not used in the experiments shown in figures 1, 2, 4 and 5.
The formation of NO2 by electrical discharges and the effect of water
Water is present in widely varying concentrations in the air in which lightning occurs. The effect of water vapour on NOx formation has been examined experimentally by Chameides et al. [1977] who found no change in total NOx yield for moist or dry air (95% and 5% relative humidity). Levine et al. [1981] found that no NO2 is formed within experimental error, although the water content of the air was not specified. Peyrous and Lapeyre [1982] examined the effect of humidity and found a significant NO2/NOx ratio, with humid air giving a lower ratio than dry air. However, it is not clear whether the NO2 was produced promptly by the spark discharges, or whether it was produced by NO from the spark reacting with the large amounts of ozone produced by the corona discharges that ran concurrently with the spark discharges.
Hill et al [1980] suggested that NO2 formation from lightning could be significant due to NO from the discharge reacting with ozone in the ambient air. As the air in the hot channel entrains the surrounding cooler air, the ozone from the entrained air reacts with NO generated by the Zel'dovich mechanism to give NO2. This behaviour was demonstrated in their computer simulations of lightning: however, to simplify the reaction scheme, the reactions of water were omitted.
The experiments reported here show both significant NO2 formation and a strong effect of water on the NO2/NOx ratio (figure 5), although water content has little effect on the total NOx formed. As a test to see if ozone in ambient air could convert NO to NO2, discharges were fired in dry air containing O3, the resulting NOx consisted mostly of NO2. If it is accepted that NO2 is formed by the reaction of O3 and NO, then the presence of water must be having a significant effect on the concentration of O3 in the air surrounding the discharge. Lightning occurs in air that has a significant water content, so it would be expected that in practice the NO2/NOx ratio would be low for atmospheric discharges.
Conclusions
The results reported here support the conclusion of Hill et al. [1979, 1980] that NOx formation by electrical discharges occurs via the Zel'dovich mechanism in the hot channel region as it cools by mixing with surrounding air. Therefore we would tend to support the calculation of Borucki and Chameides [1984] for the yield of NOx molecules per unit energy for lightning discharges of (9±2)×1016 NO molecules per joule, which was based on a cooling rate for the gases in the hot channel of ca. 400 s-1 measured by Picone et al. [1981] and their estimate that producing 1 cm3 of air at 3000 K required 1 joule of energy (equivalent to assuming that approximately 40% of the discharge energy was used to heat the gases in the hot channel to 3000 K).
The variation with spark gap, pressure and electrode size of the yield of NOx per unit energy stored on the capacitor highlights the problems of loss of energy from the hot channel gases to the electrodes. This is a potential problem for all experimental determinations of P, but is exacerbated by using smaller spark gaps, therefore we would place more reliance on the measurements of P for the larger discharges of Chameides et al. [1977] (1 m gap, P = (8±4)×1016 molecules/J) and Levine et al. [1981] (ca. 12 cm gap, P = (5±2)×1016 molecules/J). Any future experimental work on the determination of P should directly address the problem of the fraction of electrical energy that actually heats the discharge gases to ca. 3000 K.
References
Borucki W. J. and W. L. Chameides, Lightning: estimates of the rates of energy dissipation and nitrogen fixation, Reviews of Geophysics and Space Physics, 22, 363-372, 1984.
Chameides W. L., D. H. Stedman, R. R. Dickerson, D. W. Rusch and R. J. Cicerone, NOx production by lightning, J. Atmos. Sci., 34, 143-149, 1977.
Chameides. W. L., Effect of variable energy input on nitrogen fixation in instantaneous linear discharges, Nature, 277, 123-124, 1979.
Chorlton F., Textbook of Fluid Dynamics, pp271, Van Nostrand, London, 1967.
Dawson G. A., Nitrogen fixation by lightning, J. Atmos. Sci., 37, 174-178, 1980.
Drapcho D. L., D. Sisterson and R. Kumar, Nitrogen fixation by lightning activity in a thunderstorm, Atmos. Environ., 17, 729-734, 1983.
Franzblau E. and C. J. Popp, Nitrogen oxides produced from lightning, J. Geophys. Res. 94, 11089-11104, 1989.
Goldenbaum G. C. and R. R. Dickerson, Nitric oxide production by lightning discharges, J. Geophys. Res., 98, 18333-18338, 1993.
Griffing G. W., Ozone and oxides of nitrogen production during thunderstorms, J. Geophys. Res., 82, 943-950, 1977.
Hill R. D., Channel heating in return-stroke lightning, J. Geophys. Res., 76, 637-645, 1971.
Hill R. D., On the production of nitric oxide by lightning, Geophys. Res. Lett., 6, 945-947, 1979.
Hill R. D., R. G. Rinker and H. Dale Wilson, Atmospheric nitrogen fixation by lightning, J. Atmos. Sci., 37, 179-192, 1980.
Liaw Y. P., D. L. Sisterson and N. L. Miller, Comparison of field, laboratory, and theoretical estimates of global nitrogen fixation by lightning, J. Geophys. Res., 95, 22489-22494, 1990.
Levine J. S., R. E. Hughes, W. L. Chameides and W. E. Howell, N2O and CO production by electrical discharge: atmospheric implications, Geophys. Res. Lett., 6, 557-559, 1979.
Levine J. S., R. S. Rogowski, G. L. Gregory, W. E. Howell and J. Fishman, Simultaneous measurements of NOx, NO and O3 production in a laboratory discharge: atmospheric implications, Geophys. Res. Lett., 8, 357-360, 1981.
Levine J. S., T. R. Augustsson, I. C. Anderson and J. M. Hoell, Tropospheric sources of NOx: lightning and biology, Atmos. Environ., 18, 1797-1804, 1984.
Lin S. C., Cylindrical shock waves produced by instantaneous energy release, J. App. Phys., 25, 54-57, 1954.
Lutz A. E., R. J. Kee and J. A. Miller, SENKIN: a fortran program for predicting homogeneous gas phase chemical kinetics with sensitivity analysis, Sandia National Laboratories, Livermore, California, 94551, USA, 1988.
Noxon J. F., Atmospheric nitrogen fixation by lightning, Geophys. Res. Lett., 3, 463-465, 1976.
Peyrous R. and R-M Lapeyre, Gaseous products created by electrical discharges in the atmosphere and condensation nuclei resulting from gaseous phase reactions, Atmos. Environ., 16, 959-968, 1982.
Picone J. M., J. P. Boris, J. R. Greig, M. Raleigh and R. F. Fernsler, Convective cooling of lightning channels, J. Atmos. Sci., 38, 2056-2062, 1981.
Plooster M. N., Numerical simulation of spark discharges in air, Phy. Fluids, 14, 2111-2123, 1971.
Roth W., P. G. Guest, G. von Elbe and B. Lewis, Heat generation by electrical sparks and rate of heat loss to the spark electrodes, J. Chem Phys., 19, 1530-1535, 1951.
Tuck A. F., Production of nitrogen oxides by lightning discharges, Quart. J. R. Met. Soc., 102, 749-755, 1976.
Zel'dovich Ya. B., P. Ya. Sadovnikov and D. A. Frank-Kamenetskii, The Oxidation of Nitrogen by Combustion, Izdat. Akad. Nauk SSSR, Moscow, 1947.
Zel'dovich Ya. B. and Yu. P. Raizer, Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena, volume I, pp374-378, Academic Press, London, 1966.
Figure Legends
Figure 1. Deflection of laser beam by shock front: laser beam 6 (lower) and 12 (upper) mm from discharge, 20 mm spark gap, 500 mbar pressure, discharge energy 113 J, energy per unit length 5.7×103 J m-1.
Figure 2. Distance travelled by shock front, : 20mm spark gap, discharge energy 113 J, energy per unit length 5.7×103 J m-1, : 4mm spark gap, discharge energy 42 J, energy per unit length 1.1×104 J m-1, 500 mbar pressure.
Also shown for comparison is the radial propagation of the shock front as calculated by Hill [1971] (-------- 1013 mbar pressure, 1.4×104 J m-1) and Lin [1954] (-- -- -- = 1.4, 500 mbar, 5.7×103 J m-1).
Figure 3. NOx freeze out mixing ratio (27 mbar pressure, 20 mm spark gap, 100 J discharge energy (with thyratron in circuit) energy per unit length 5×103 J m-1).
Figure 4. Variation of NOx yield per unit energy with spark gap ( : Chameides et al. [1977], : Levine et al. [1981], : Peyrous and Lapeyre [1982], = : this work, 400 mbar pressure, discharge energies 31 - 84 J, energy per unit length 4.2×103 - 7.8×103 J m-1).
Figure 5. Variation in NOx yield (+) and NO2/NOx ratio () with water content of air (8 mm spark gap, 400 mbar pressure, discharge energy 38 J, energy per unit length 4.7×103 J m-1)
Figure 6. Variation of NO equilibrium mixing ratio and tauequil. with temperature (-------- 500 mbar, -- -- -- 27 mbar). The calculations were made using the NO and NO2 reaction scheme of Hill et al. [1980] and integrated using the SENKIN program [Lutz et al., 1988], with constraints of constant temperature and pressure. tauequil. is defined here as the time for the NO concentration to reach half the equilibrium value.




Figure 1. Deflection of laser beam by shock front: laser beam 6 (lower) and 12 (upper) mm from discharge, 20 mm spark gap, 500 mbar pressure, discharge energy 113 J, energy per unit length 5.7×103 J m-1.
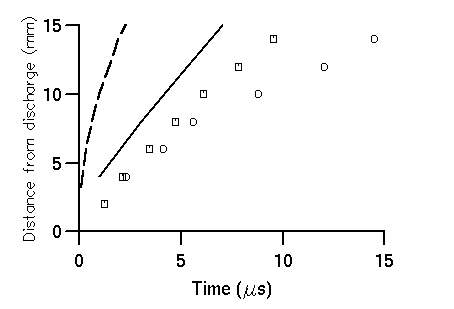 Figure 2. Distance travelled by shock front, : 20mm spark gap, discharge energy 113 J, energy per
unit length 5.7×103 J m-1 : 4mm spark gap, discharge energy 42 J, energy per unit length
1.1×104 J m-1, 500 mbar pressure.
Figure 2. Distance travelled by shock front, : 20mm spark gap, discharge energy 113 J, energy per
unit length 5.7×103 J m-1 : 4mm spark gap, discharge energy 42 J, energy per unit length
1.1×104 J m-1, 500 mbar pressure.
Also shown for comparison is the radial propagation of the shock front as calculated by Hill [1971] (-------- 1013 mbar pressure, 1.4×104 J m-1) and Lin [1954] (-- -- -- = 1.4, 500 mbar, 5.7×103 J m-1).
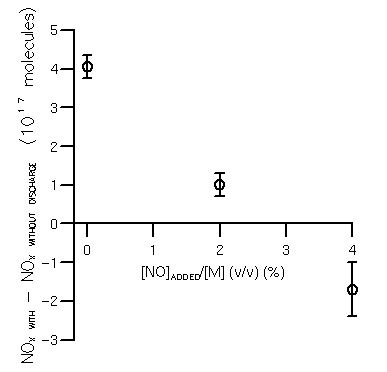 Figure 3. NOx freeze out mixing ratio (27 mbar pressure, 20 mm spark gap, 100 J discharge energy
(with thyratron in circuit) energy per unit length 5×103 J m-1).
Figure 3. NOx freeze out mixing ratio (27 mbar pressure, 20 mm spark gap, 100 J discharge energy
(with thyratron in circuit) energy per unit length 5×103 J m-1).
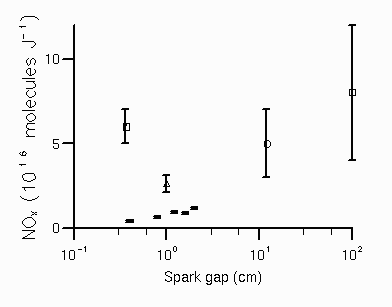 Figure 4. Variation of NOx yield per unit energy with spark gap ( : Chameides et al. [1977], :
Levine et al. [1981], : Peyrous and Lapeyre [1982], = : this work, 400 mbar pressure,
discharge energies 31 - 84 J, energy per unit length 4.2×103 - 7.8×103 J m-1).
Figure 4. Variation of NOx yield per unit energy with spark gap ( : Chameides et al. [1977], :
Levine et al. [1981], : Peyrous and Lapeyre [1982], = : this work, 400 mbar pressure,
discharge energies 31 - 84 J, energy per unit length 4.2×103 - 7.8×103 J m-1).
 Figure 5. Variation in NOx yield (+) and NO2/NOx ratio () with water content of air (8 mm spark
gap, 400 mbar pressure, discharge energy 38 J, energy per unit length 4.7×103 J m-1)
Figure 5. Variation in NOx yield (+) and NO2/NOx ratio () with water content of air (8 mm spark
gap, 400 mbar pressure, discharge energy 38 J, energy per unit length 4.7×103 J m-1)
 Figure 6. Variation of NO equilibrium mixing ratio and tauequil. with temperature (-------- 500 mbar,
-- -- -- 27 mbar). The calculations were made using the NO and NO2 reaction scheme of
Hill et al. [1980] and integrated using the SENKIN program [Lutz et al., 1988], with
constraints of constant temperature and pressure. tauequil. is defined here as the time for the NO
concentration to reach half the equilibrium value.
Figure 6. Variation of NO equilibrium mixing ratio and tauequil. with temperature (-------- 500 mbar,
-- -- -- 27 mbar). The calculations were made using the NO and NO2 reaction scheme of
Hill et al. [1980] and integrated using the SENKIN program [Lutz et al., 1988], with
constraints of constant temperature and pressure. tauequil. is defined here as the time for the NO
concentration to reach half the equilibrium value.
Figure 1. Deflection of laser beam by shock front: laser beam 6 (upper) and 12 (lower) mm from discharge, 20 mm spark gap, 500 mbar pressure, discharge energy 113 J, energy per unit length 5.7×103 J m-1.